Introduction
Imagine that an artificially intelligent robot approaches a valley. Looking down the cliff into the valley, the robots sees a large, man-made, labyrinth structure. The structure has an entrance, an exit, and is surrounded by water. The robot can, of course, simply enter the structure and wander around, until it finally reaches an exit point. However, since the robot is programmed with AI, it can do a lot better.
The robot can scan the maze into its memory and perform image processing against it, converting the pixels in the image into a data representation of the maze. With the maze analyzed, an algorithm can be ran against it to determine a solution path through the maze. All of this can be done within seconds. Once complete, the robot can simply walk through the maze in one try.

By the way, if you want to skip right to the good stuff and just play with mazes, then head over to the javascript maze solver. Otherwise, read on.
There are many methods for solving a maze and performing a pathfinding search. For our robot, we’ll consider two cases.
In the first case, let’s assume the robot is standing on a cliff. The robot will be able to see the entire maze, including the entrance and exit, and can fully process it to find a solution path. Lacking a cliff, perhaps the robot can eject a nanobot overhead, quickly taking a snapshot of the terrain, and sending the image back to the robot to process. In this case, the robot has no need to physically perform the search algorithm itself, methodically moving down each path and backtracking, as it searches to reach the exit. The robot can do all of this within its CPU.
In the second case, we’ll assume the maze is inside a mountain or underground, concealing the inner tunnels from sight. In this case, the robot will be unable to pre-process the tunnels with an algorithm and will be forced to physically enter the maze (or at least send in a probe) to scout a solution path.
Bird’s Eye Imagery Available
Assuming the robot has an aerial layout of the maze, the AI may choose to use A* or Tremaux pathfinding search algorithms. There are a variety of other maze algorithms available as well, but we’ll be discussing these two in detail.
With a layout of the maze provided, both A and the Tremaux algorithm will provide a successful path through the maze. [A Search](http://en.wikipedia.org/wiki/A*_search_algorithm) works better on mazes with non-uniform tiles and obstacles within the paths (such as large paths to walk on, open areas, fallen rocks, etc), while Tremaux works better on complex “classic” style mazes (fixed-size pixel tiles) with many passages in many directions. Using either algorithm, the AI will determine a solution and may successfully traverse the maze.
For our second case, our robot does not have the luxury of a layout view of the maze. In this case, the robot will have to search the hard way - physically traversing the tunnels to find the exit. However, it can still be smart.
No Imagery Available
The robot is on the ground and sees the entrance tunnel before him. No aerial layout is provided and, in addition, the robot has no knowledge of the exit point. He’ll need to enter the maze and traverse the paths in real-time in order to find the exit.
In this scenario, A search will not be possible, since it requires knowing the exit location in order to make its heuristic calculation. At each step, A calculates which tile in the path is the next best move, getting closer and closer to the exit. It determines this by a calculation on the exit tile and the neighboring tiles. Common heuristics are the manhattan distance (difference in X + difference in Y to the target tile) or the diagonal distance (maximum of the difference in X and the difference in Y to the target tile).
With A* search out of the picture, the robot can choose an alternative, such as the Tremaux algorithm. This method is similar to actually walking through the maze. Only the immediate tiles visible to you can be followed. The robot begins walking in a random direction and continue until it hits a wall. It then turns right, until a path is available to walk. Each time the algorithm takes a step, it marks the tile as visited. The algorithm always tries to first visit an unvisited tile. However, if no new tiles are found, it will backtrack over a visited tile, incrementing the mark on the tile to 2, until it finds an unvisited tile. It will never visit the same tile more than twice (with the only exception being if the algorithm is stuck in a dead-end, in which case it will re-visit a tile it’s already backtracked over, in order to exit the trap. The maze solution is all tiles that have been visited just once.

Printing the Solution
With the Tremaux algorithm, the solution path consists of all tiles that have been visited once, as shown below:
1 | // Print the solution path. |
In contrast, with the A* search algorithm, the solution consists of the “solution” set. This set is found by walking backwards, along the shortest path, from the exit point to the origin tile.
1 | // Compile the solution path. |
A* Search Heuristics
Note, in order for the AI to use A* search to find a solution path, it requires knowing the exit point. It uses this data in its heuristic calculation, as shown below (where pos0 is the current tile and pos1 is the exit tile).
Manhattan Distance
1 | this.manhattan = function(pos0, pos1) { |
Diagonal Distance
1 | this.diagonalDistance = function(pos0, pos1) { |
Without this information, we can still solve the maze using other techniques, although (sometimes) not as fast.
Intelligence Requirements
In order to find a path through a maze, A* search and the Tremaux algorithm both have specific criteria that must typically be met. Both algorithms assume that the maze is solvable (ie., there is an entrance and an exit). Tremaux requires that each tile in the path is 1-unit in size with no obstructions in the path, other than walls. That is, the maze must contain well-defined, narrow passages. Tremaux does not require knowing the exit point when beginning the search through the maze. Since it essentially performs a depth-first search, it simply needs to know when to stop (ie., when an exit tile is visited).
A search tends to be more flexible and is usually able to search around obstacles and variable-sized paths. However, A has other requirements and limitations. It must know the exit point before beginning its calculations. It also needs an explicit heuristic defined. Movement with an A search algorithm is typically 4-directional or 8-directional, including diagonals. Consider the following example of A search using only horizontal and vertical movement vs including diagonals:
A* Search - No Diagonals
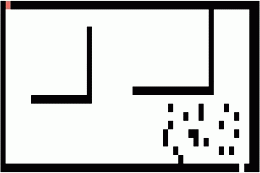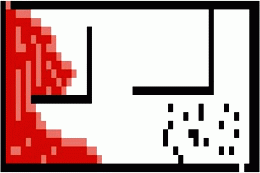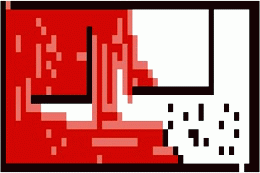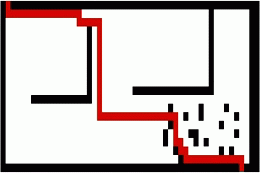
A* Search - With Diagonals
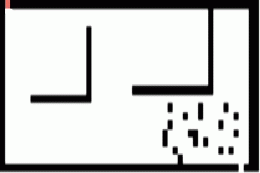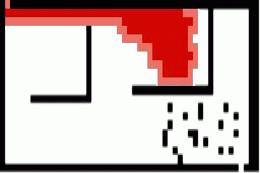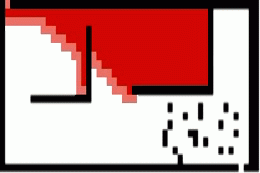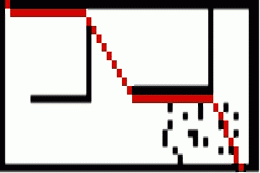
Search Speed and Maze Complexity
While both algorithms will find a solution to a maze, each does better, depending on characteristics of the maze. In the following maze, shown below, Tremaux performs a more direct search to locate the solution (leaving more of the map unsearched). A* search takes longer, exploring almost all of the map to locate a solution. This is most likely due to the directions of the maze tunnels leading away from the exit point and the high-degree of backtracking required.
A* Search Solving a Complex Maze

Tremaux Algorithm Solving a Complex Maze

Try It Yourself
Experiment with various mazes, using the Tremaux and A* search algorithms or even build your own. The JavaScript maze solver allows selecting either maze solving algorithm and runs it against the selected map. Maps can be created on-the-fly by passing a JSON object in the url. See the instructions on the demo for details.
Download @ GitHub
Like what you see? All source code for the project is available on GitHub. This includes the demo page and dynamic selection of mazes.
About the Author
This article was written by Kory Becker, software developer and architect, skilled in a range of technologies, including web application development, machine learning, artificial intelligence, and data science.
Sponsor Me