Intelligent Topic Detection with Unsupervised Learning

Introduction

Artificial intelligence learning generally consists of two main methods. These include supervised and unsupervised learning. Supervised learning involves using an existing training set, which consists of pre-labeled classified rows of data. The machine learning algorithm finds associations between the features in the data and the label (or output) for that row. In this manner, a machine learning model can predict on new rows of data, that it has never been exposed to prior, and return an accurate classification based upon its training data. Supervised learning can work great for large data sets where you already have pre-classified data readily available.

At the other end of the spectrum is unsupervised learning. With this type of learning, data does not need to be pre-labeled or pre-classified in a training set. Instead, the machine learning algorithm finds similar features and associations amongst the features in the data and groups them together accordingly. For example, two pieces of data might appear similar, according to certain features, and would therefore be grouped into the same box (more formally called a “cluster”). By clustering the similar data together, you can then predict the clusters for new rows of never-before-seen data and obtain an accurate classification. Unsupervised learning can work well for sets of data where some form of common associations exist. It also benefits from the fact of not requiring a pre-labeled training set, which is often one of the more difficult parts of supervised learning (often requiring manual human labeling of training data).

Similar to the method of supervised learning, unsupervised learning and clustering can utilize training data to formulate groupings. Where supervised learning uses pre-labeled training sets, unsupervised learning needs only the data. Naturally, pre-labeling training data for supervised learning is both time-intensive and prone to human error. For these reasons, by not requiring (manual/automated/human) pre-labeled data sets, unsupervised learning has the potential to bring advances in machine learning and artificial intelligence results.

In this tutorial, we’ll walk through a demonstration of using unsupervised learning and clustering to intelligently identify color points plotted on a graph, as being red, green, or blue in overall color. For example, a point that has the color purple might be considered red or blue. Our unsupervised learning algorithm will learn to detect points like this as a specific color category. We’ll also see the results of running the K-Means algorithm to cluster training data, identify cluster centers, label existing data, and predict categories for new data. Finally, you’ll see how to apply unsupervised classification to other types of data (beyond colors!), including classifying stock and bond ETF funds under specific categories. We’ll use R as the programming language, of course, you can also use JavaScript or any language of your choice for the examples.

After completing this tutorial, you’ll have an understanding of how to apply unsupervised machine learning to a variety of topics, including other numerical data, industry specific topics, natural language processing, and even text.

A Bunch of Pretty Colors

Let’s start this tutorial off by generating a bunch of different colors. Naturally, colors consist of a red, green, and a blue value. By combining these three values together we can obtain a variety of colors. The color pure red is identified by the red, green, and blue (RGB) values of rgb(255, 0, 0). Similarly, all three pure color values are listed below.

rgb(255, 0, 0) // Red
rgb(0, 255, 0) // Green
rgb(0, 0, 255) // Blue

Varying degrees of red, green, and blue colors can be represented by adjusting their values respectively. For example, rgb(255, 0, 255) consists of a lot of red and a lot of blue, resulting in the color purple.

What Exactly Are We Classifying?

So far, we’ve discussed how to generate colors by combining red, green, and blue values. Now that we can create colors, how can a machine learning algorithm help?

Recall that our color purple could actually be considered red or blue. In fact, since both the red and blue values for our purple example consist of the max value rgb(255, 0, 255), labeling this color as red or blue would both be correct. However, what if we slightly reduce the blue value. The color would still appear purple to the human eye. However, it could probably be more accurately classified under red, now.

Here are some examples of how colors might be grouped.

rgb(200, 0, 150) // Purple Plum => Red
rgb(50, 199, 135) // Sea Green => Green
rgb(100, 180, 255) // Sky Blue => Blue

With the above type of classification idea, we can utilize machine learning to see if it can identify these groups of colors all by itself. While we have an idea of which colors should be red (the ones with a higher red value in their rgb() combination), let’s see if the computer can, likewise, identify these groups of colors and accuractly place rgb values into their natural respective grouping.

Thinking About Colors

It’s a lot easier (and more fun!) to think about how colors can be clustered together by viewing them on a graph. In this manner, we can plot the colors on a graph, grouping them together by their respective red, green, and blue values, and get an idea of how the colors naturally form layers of clusters. It’s up to our machine learning algorithm to draw the boundaries, of course, for where a color is red versus green versus blue, but the human eye can still get an overall idea.

Generating Random Colors

First, let’s take a look at some code to randomly generate colors and plot them on a chart. We’ll need to generate random values for red, green, and blue. We’ll also need to translate the rgb() values into a hexadecimal format, in order to render the color on the chart. Luckily, R makes it easy to convert rgb into hex, simply by calling the following line of code:

rgb(255, 100, 175, maxColorValue = 255)

The above code results in the value #FF64AF, which is an HTML-compatible color that we can plot on a chart.

Converting RGB to a Numeric Value

In addition to simply generating colors, we’ll need a way to plot the 3D colors on a 2D chart. That is, our colors consist of a red, green, and blue value. However, plotting on a chart requires an x,y value. Therefore, we’ll need a way to convert the 3D red, green, blue value into a numerical feature.

We can convert our colors into numerical values by simply multiplying their respective red, green, blue values by the max value and indexing accordingly. We can use the following formula:

(Red * 256 * 256) +
(Green * 256) +
(Blue)

Using the above formula, we get the following values for these example colors:

rgb(200, 0, 150)
// 13107350

rgb(50, 199, 135)
// 3327879

rgb(100, 180, 255)
// 6599935

Notice how the red colors form a much larger numeric value. This will result in reds being plotted towards the top of the chart, if using the y-axis for plotting the values. Likewise, blue values have a smaller range of values, resulting in them falling towards the bottom of the chart. Green colors sit in the middle.

Now that we have a way to generate random colors and convert them to a numeric representation, we can plot them on a chart. We can then classify them with unsupervised learning and see where the computer decides to draw the boundaries between colors, effectively grouping each color into a cluster of red, green, or blue.

Plotting Colors on a Chart

We can use the following R code, shown below, to generate a set of random colors and convert them to a numerical representation.

rgb2Num <- function(data) {
  # Maps RGB colors to a single value.
  result <- sapply(1:nrow(data), function(row) {
    color <- data[row,]
    (color$red * 256 * 256) + (color$green * 256) + color$blue
  })
  
  result
}

generateColors <- function(n) {
  # Generate a set of random colors.
  colors <- as.data.frame(t(sapply(1:n, function(i) {
    parts <- sample(0:255, 3)
    c(red = parts[1], green = parts[2], blue = parts[3], hex = rgb(parts[1], parts[2], parts[3], maxColorValue = 255))
  })), stringsAsFactors = F)

  # Convert to numeric values.
  colors$red <- as.numeric(colors$red)
  colors$green <- as.numeric(colors$green)
  colors$blue <- as.numeric(colors$blue)
  
  # Map each color to an x/y-coordinate for easy plotting.
  colors$x <- 1:nrow(colors)
  colors$y <- rgb2Num(colors)

  colors
}

The above code simply generates random numbers from 0-255 for each red, green, and blue value. It then generates the HTML-color hexadecimal value for each color and calculates the Y-axis value using the simple formula described earlier. For the X-axis, we’ll simply use the index of the color (1-1000, for 1,000 generated colors), since we’re really only interested in where the colors fall. In this manner, the colors will be plotted top to bottom, with respect to their red, green, blue values, and plotted across the graph simply based on their index.

Below is an example of the training data, produced by running the code shown above.

> generateColors(10)
   red green blue     hex  x        y
1  186   160  122 #BAA07A  1 12230778
2   40     2  114 #280272  2  2622066
3  126    99  118 #7E6376  3  8282998
4  182    14   90 #B60E5A  4 11931226
5  205   213   60 #CDD53C  5 13489468
6   90   218  216 #5ADAD8  6  5954264
7   75    37  178 #4B25B2  7  4924850
8   26     8  253 #1A08FD  8  1706237
9    8    86  232 #0856E8  9   546536
10 158    73  187 #9E49BB 10 10373563

You can see how we can now easily plot this data on a chart by using the x,y values generated from the red, green, and blue values.

Beautiful Colors

Here are what 1,000 randomly generated colors look like when plotting on a chart according to their respective values.

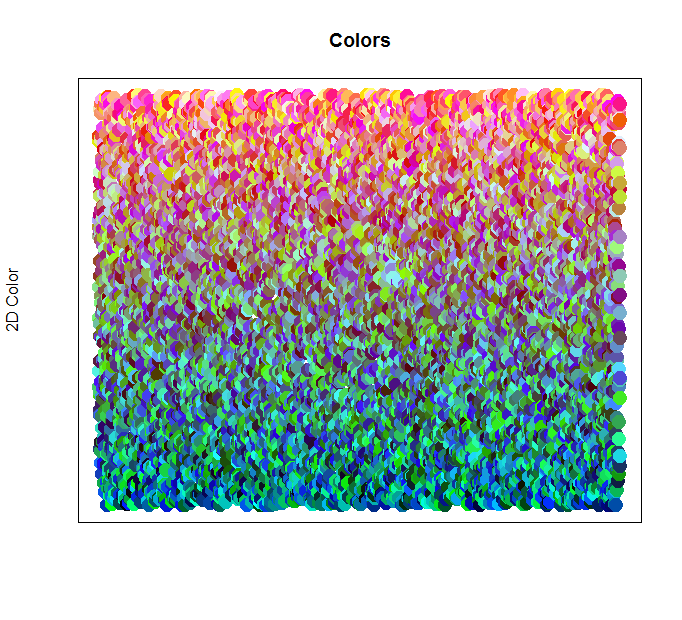
As you can see in the above image, the blue colors are grouped largely along the bottom, followed by the green colors. Notice how the green colors melt into both the blue and red, using varying degrees of orange and teal as they move closer to each boundary. It’s difficult to draw a clear cut line between where green ends and red starts. Likewise, the start and end of blue versus green is also difficult to determine. This type of classification is where a machine learning and artificial intelligence algorithm can really excel.

Since machine learning uses numerical features within the data to form associations and classifications, it can determine a set boundary from which to classify the colors into their respective grouping or cluster.

Less Color and More Machine Learning

Plotting 1,000 colors with our grouping formula certainly creates a beautiful image. However, let’s consider a smaller set of data of just 100 colors. This will make it easier to view the data and their eventual classifications under red, green, and blue clusters.

Below is our training data, consisting of 100 randomly generated colors, plotted on a graph according to their respective values.

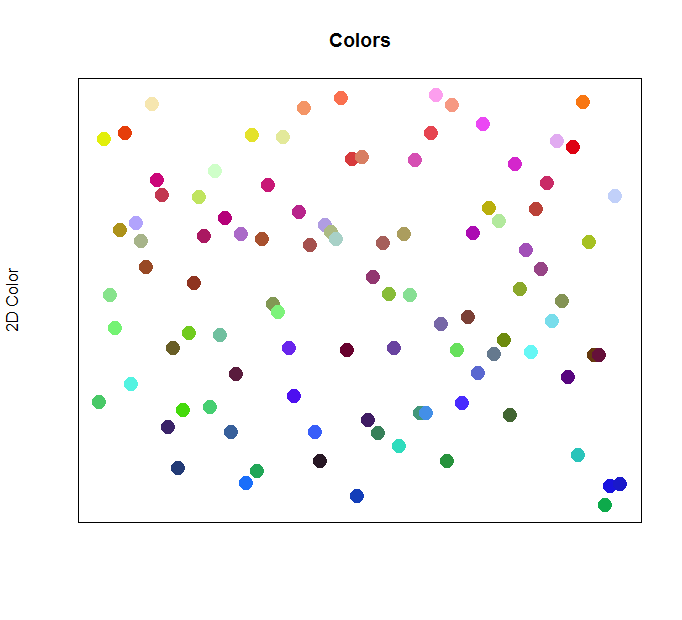
The above image of 100 colors is really no different than our 1,000 colors. Notice how the blue points tend to fall along the bottom of the graph, green and yellows in the middle, and red points towards the top. Let’s take a look at how we can apply an unsupervised machine learning algorithm to classify and label each point according to the color.

Clustering Colors into Groups

The most common algorithm used for clustering data into groups is the K-Means algorithm. This clustering algorithm groups data into k clusters, based upon how similar the features for each data point are to one another.

We can apply the K-Means clustering algorithm to the color points in order to group them together, according to their respective red, green, and blue color values. The K-Means algorithm works by initially setting random center points amongst the data. It then groups all points that are closest to each center into a single cluster. The center of each cluster is then shifted to the center of the associated points. We then repeat the process by re-assigning all points to their closest center until the centers of each cluster no longer changes (or the change is less than a certain threshold). At this point, the unsupervised training is complete.

It can help to view a visualization of the K-Means algorithm to get a better understanding of how the steps work.

K-Means Clustering

A complete listing of the K-Means unsupervised learning algorithm steps are shown below.

1. Determine the number of clusters (i.e., the K value). A rule of thumb for choosing the number of clusters is to take the square root of the number of data points divided in half. An example of this is shown below.
2. Randomly initialize the centroids (i.e., centers) for each cluster.
3. Assign each point in the data to the cluster with the closest center to it.
4. Shift the centroids for each cluster to the mean (center) of all points assigned to it.
5. Repeat steps 3-5 until the centroids stop moving, or the points stop switching clusters, or a given threshold is reached.

Example code for determining the number of centroids for clustering is shown below.

K = ~~(Math.sqrt(points.length * 0.5));

Calculating Centroids

Let’s apply the K-Means algorithm to our set of color data points and see where the cluster centroids fall. Normally, you would try to guess at a suitable number of clusters to utilize, such as by using the rule of thumb algorithm mentioned above. However, since we know we’re looking for a classification of red, green, or blue for our data points, we can choose a K value of 3, for 3 cluster groups.

We can run the K-means algorithm on our collection of color data points with the following code shown below.

# Run kmeans clustering on the data.
fit <- kmeans(train[,1:3], 3, nstart = 20)
train$group <- fit$cluster

In the above code, notice that we’re only selecting the first 3 columns in our data. This corresponds to the columns red, green, and blue, as those are the 3 features that we want to train against. The other columns in our data set correspond to coordinates for plotting on the graph and drawing colors.

The second line of code simply sets the cluster group that each data point has been assigned to after running the algorithm.

With the clustering completed, we can peek at the results of the process to view details on the centroids.

K-means clustering with 3 clusters of sizes 24, 33, 43

Cluster means:
        red     green      blue
1  98.16667  64.66667 189.20833
2 164.18182  65.03030  64.72727
3 140.67442 196.58140 132.20930

Clustering vector:
  [1] 3 3 3 3 2 2 3 3 3 2 3 2 2 1 2 1 3 3 2 3 2 3 3 3 2 1 2 1 1 3 3 2 2 3 3 3 1 1 2 3 2 1 2 3 3
 [46] 3 2 2 2 1 2 1 2 3 2 3 1 3 3 3 1 3 1 2 3 1 3 3 3 1 2 1 1 1 2 1 3 2 2 1 3 1 3 2 2 2 3 3 3 1
 [91] 2 3 2 3 2 2 3 1 3 1

Within cluster sum of squares by cluster:
[1] 182410.6 201096.4 443809.0
 (between_SS / total_SS =  46.1 %)

Notice above, our algorithm has completed with 3 clusters of size, 24, 33, and 43 respectively (which total to 100 data points). This represents the number of color points that were assigned to each cluster. So, 24 data points were assigned to the first cluster, 33 to the second, and 43 to the last.

We can also see the mean values for each of the features within each cluster. Remember, we have 3 feature values for each data point (values between 0-255 for red, green, and blue) and we’ve trained for 3 clusters. Therefore, each centroid will also have a red, green, and blue value corresponding to the mean of their associated data points that were assigned to their cluster. This will appear much more intuitively once we draw the centroids on the graph.

At this point, we have 3 clusters trained on the data. All of our data points have been assigned to a cluster. However, the clusters don’t actually have a “name”. We can’t call the first cluster “Our Red Group”, since we don’t yet know what type of data has been assigned to it (actually, we can peek at the mean values for the centroids and take a guess at the name for each cluster; for example, the first cluster has the mean values rgb(98, 64, 189)) which is purple in color or can be considered blue; likewise the second cluster is rgb(164, 65, 64)) which is red; the last cluster is rgb(140, 196, 132)) which is green).

Let’s plot each cluster centroid on the graph, right on top of the color points. This will let us see where each cluster center lies and provide us with a way to formally label the clusters with names.

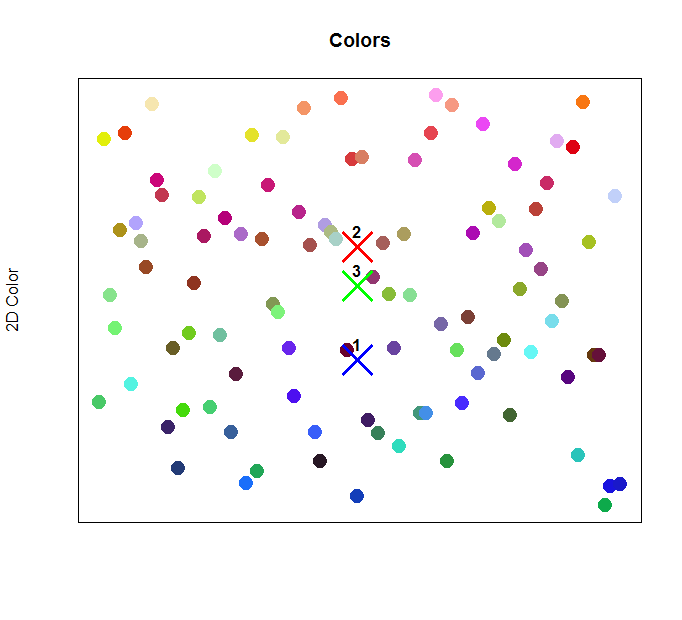
In the image above, we’ve plotted the centers for the 3 trained clusters on top of the color data points. As we’ve predicted from the results of the clustering output, cluster 1 is indeed within the blue range of points, along the bottom of the graph. Cluster 2 is the highest on the graph, corresponding to the reds. Cluster 3 sits right in the middle, corresponding to the green values. So far, so good!

At this point, we can name our clusters as follows:

Cluster 1 - "Blue Group"
Cluster 2 - "Red Group"
Cluster 3 - "Green Group"

Classifying Colors to a Cluster

Let’s look at each color data point and see which exact cluster each one has been assigned to. Recall, after training, we set the cluster number that each data point was assigned to. In this manner, our training set now has an additional column, containing the assigned cluster number. With this piece of data, we can plot each data point’s cluster on the graph, as shown below.

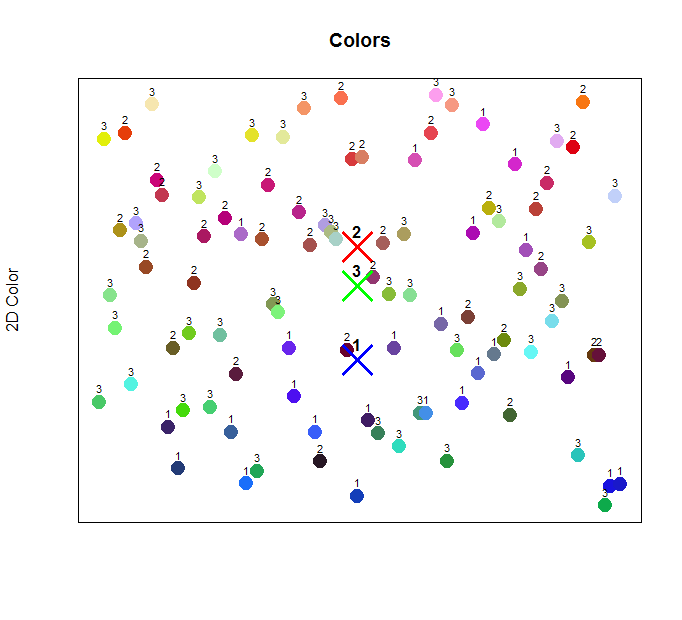
The above image labels each data point with its assigned cluster. We’ve already plotted the cluster centers on the graph, but now we’re showing each point’s actual assignment as well.

Notice how most of the blue-ish points along the bottom were assigned to cluster 1 (“Blue Group”). There are also a few points along the bottom of the graph that were assigned to cluster 3 (“Green Group”). Remember, we’re drawing the colors on the graph according to a simple math formula that converts the raw red, green, and blue value into a numerical value. However, the clustering works differently, via calculating means to the centers of each cluster.

For example, look at the points along the bottom of the graph that were labeled as 3 (“Green Group”). Their colors range from green/blue to cyan, to teal, all of which include green-ish and blue-ish hues. It makes sense to classify these points within either the Blue or Green group.

Likewise, there are some points along the top of the graph that were not assigned to cluster 2 (“Red Group”), but were instead assigned to cluster 1 or 3. For example, some of the points assigned to cluster 3 are yellow. They were plotted at the top of the graph due to their numerical value from our simple formula, but they were grouped into the “Green” cluster because their rgb value still lies within the range of the trained “Green” group. After all, yellow sits right next to green in the color scale.

This difference in location of the plotted coordinate of each color and their assigned color becomes much more apparent if we plot each color directly within their assigned cluster. This will allow us to view each color, plotted in a single line, according to their assigned cluster.

Grouping Colors into their Cluster

Let’s see which color points were assigned to which cluster in a more visual way. Rather than plotting the data points along the y-axis according to our simple numerical calculation of red, green, blue, we can instead plot according to their assigned cluster. We’ll plot each point on a single line along the x-axis, with their assigned cluster for the y-axis.

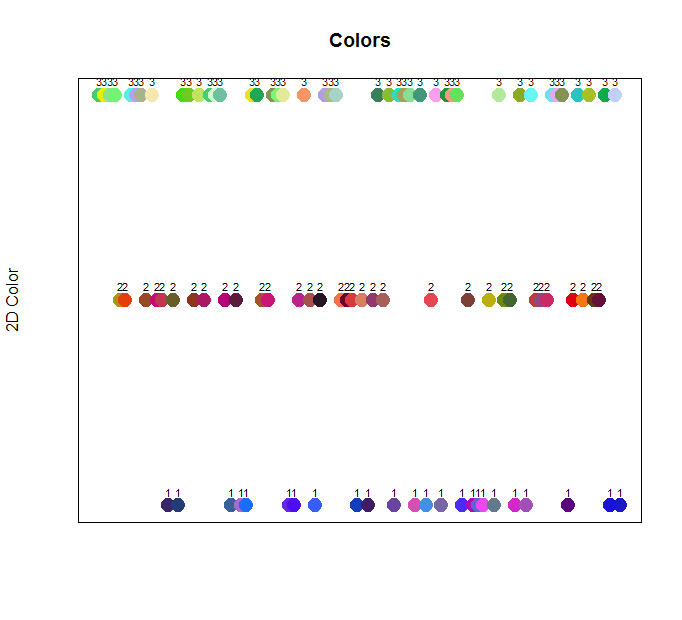
The above image makes it much more apparent how the colors were grouped together during training. Sure enough, all of the blue values are grouped into cluster 1 (“Blue Group”). This includes purple and pink colors as well (which may have previously been plotted in the top of the graph [i.e., in the red zone] when using our simple numerical calculation for the y-axis).

Likewise, the reds and yellows are plotted in cluster 2 (“Red Group”). This includes browns and even some yellow-greens as well. Finally, the greens, light blues, and even some light pinks that are somewhat closer to green in color, were plotted in cluster 3 (“Green Group”).

Predicting on New Data

Now that we’ve trained our unsupervised machine learning algorithm using K-means clustering, we have a way of labeling color data points to a specific cluster. We’ve labeled each cluster according to their contents as “Blue Group”, “Red Group”, and “Green Group” respectively.

The big test is to now predict the assigned group of a new data point that the algorithm has never seen before. Will it predict the correct color group for the color point in question?

Let’s generate three new random color points. We’ll then ask the model to classify each one to a cluster.

test <- generateColors(3)

The above code generates 3 new colors, as shown below.

  red green blue     hex x        y
1 232    17  252 #E811FC 1 15208956
2  86   109  216 #566DD8 2  5664216
3  67   219  216 #43DBD8 3  4447192

Using our already trained model (i.e., the calculated centroids), we can determine which cluster each point would be assigned to. In R, we can use the kcaa library to predict on an already trained k-means algorithm, as shown below.

# Cast the k-means model to be of type kcaa, so we can use the predict method.
fit2 <- as.kcca(fit, data=train[,1:3])

# Predict the assigned color by mapping the color to a cluster.
group <- predict(model, newdata=data[,1:3])

# Assign the label of the cluster.
data$label <- sapply(1:nrow(data), function(row) {
centroids[centroids$group == data[row, 'group'], ]$label
})

In the above code, we’re simply casting our k-means model fit to the type kcaa so that we can call the prediction method. After casting, we can then call predict, passing in our already trained model, along with the data points to make a prediction on.

After predicting the cluster number, we can then assign the given cluster name to each data point, for a more human-readable cluster assignment on the predicted data.

We get the following results for this data, shown below.

  red green blue     hex x        y group label
1 241    52   11 #F1340B 1 15807499     2   red
2  80   187  139 #50BB8B 2  5290891     3 green
3  34    15  194 #220FC2 3  2232258     1  blue

Notice, the first point was assigned to cluster 2 (“Red Group”). This makes sense, since the red value is the largest value. The second point was assigned to cluster 3 (“Green Group”), and sure enough, its green value is the largest value. The last point was assigned to cluster 1 (“Blue Group”), again due to its blue value being the largest value.

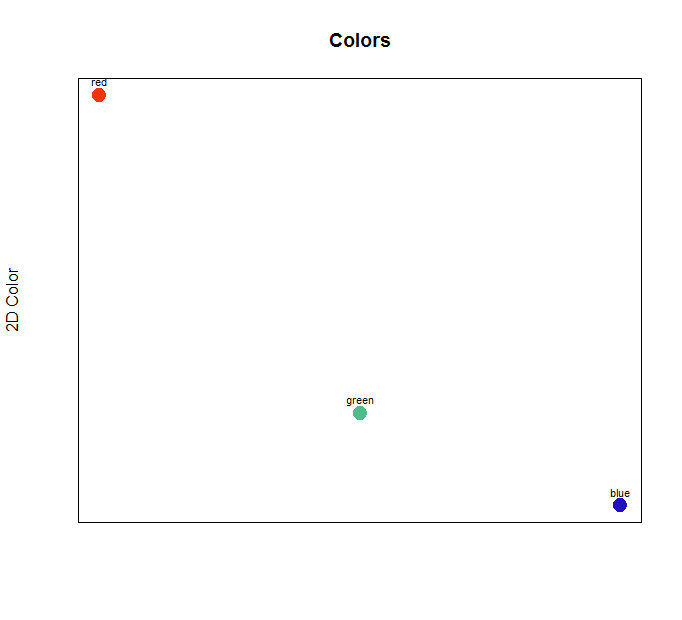
The above image shows the predicted cluster group for the three new data points. These randomly generated colors (red, green, and blue to the human eye) were indeed assigned to the Red, Green, and Blue group respectively.

Beyond Colors

Clustering colors is a neat way to visualize and understand how unsupervised machine learning in artificial intelligence works. However, we can take unsupervised learning beyond this subject, to more real-world scenarios.

Let’s apply the same unsupervised learning clustering method to the financial sector, using AI to automatically categorize stock ETFs under specific groupings and categories.

Using AI to Categorize ETF Stock and Bond Funds

We’ll start by locating a data source, containing a list of Exchange Traded Funds (ETF), corresponding to stock and bond funds. ETF funds are similar to mutual funds, and typically target specific sectors within the financial industry, such as energy, technology, the S&P 500, international, treasury bonds, etc.

We’ll attempt to use artificial intelligence unsupervised learning to automatically categorize a listing of ETF funds, based on their Year to Date (YTD), 1-Year, 5-Year, and 10-Year percentage returns. Can the AI find similarities amongst the ETF funds within similar categories and group them accordingly, based solely on these features? Let’s apply clustering and find out!

The Data Source

For the data source we’ll use the listing of Vanguard ETF funds. An excerpt from the ETF description data on the web site is shown below in tab-separated format.

Ticker  AssetClass  ExpenseRatio    Price   Change1 Change2 SECYield    YTD Year1   Year5   Year10  Inception
VCR Stock - Sector  0.10%   $140.79 -$0.14  -0.10%  1.29%B  10.14%  18.24%  17.06%  9.90%   9.35% (01/26/2004)
VDC Stock - Sector  0.10%   $138.44 -$0.39  -0.28%  2.46%B  4.68%   2.60%   12.80%  10.33%  10.27% (01/26/2004)
VIG Stock - Large-Cap Blend 0.08%   $92.39  -$0.21  -0.23%  1.93%B  9.62%   13.75%  12.75%  7.41%   7.92% (04/21/2006)
VWOB    International   0.32%   $79.42  $0.03   0.03%   4.32%A  4.76%   4.51%   —   —   4.70% (05/31/2013)
VDE Stock - Sector  0.10%   $88.06  $0.49   0.56%   2.69%B  -14.68% -4.55%  0.64%   0.65%   6.52% (09/23/2004)

From the above ETF data, we have the following list of features available to us.

1. Ticker
2. Asset Class
3. Expense Ratio
4. Price
5. Change 1
6. Change 2
7. SEC Yield %
8. Year to Date %
9. 1 Year %
10. 5 Year %
11. 10 Year %
12. Earnings Since Inception

We could select a variety of these features to use for clustering. In fact, any of the features (even text) can be converted into numerical representations to utilize for unsupervised learning. However, for this example, we’ll narrow down the feature selection to just the year percentage returns.

Using the above data, we’ll attempt to cluster based upon columns 8-11 (YTD, Year 1, Year 5, Year 10 percentage returns). Let’s take a quick look at the overall process.

Steps for Clustering ETF Funds

Just as we did with colors, we’ll follow a very similar process for grouping the ETFs under categories. Specifically, we’ll follow the steps listed below.

1. Read the data source, containing ETF fund information.
2. Clean the data, converting percentage and dollar amount strings to numerical values.
3. Split the data into a training and testing set.
4. Run K-means clustering on the training set.
5. Set the calculated cluster group for each row of data in the training set. This let’s us understand the results.
6. Manually label the clusters with names, by examining the data that was assigned to each cluster (we’ll use the categories: “International”, “StockBigGain”, “Stock”, “Bond”, and “SmallMidLargeCap”).
7. Predict the categories for the test set by applying the model against new data, and set the resulting cluster name on each row of test data.
8. Manually examine the results and see if the categories make sense.

Categorizing ETFs with Clustering

We’ll start by loading the packages in R in the same manner as we did for clustering colors. Next, we’ll load the tab-separated (tsv) file, containing our ETF description data, and convert the percentage and dollar-amount strings into numerical values, essentially cleaning the data. The code is shown below.

packages <- c('flexclust', 'caTools')
if (length(setdiff(packages, rownames(installed.packages()))) > 0) {
  install.packages(setdiff(packages, rownames(installed.packages())))  
}
library(flexclust)
library(caTools)

# Read the data set. Source: https://investor.vanguard.com/mutual-funds/list#/etf/name/month-end-returns
data <- read.csv2('vanguard-etf.tsv', header=T, sep='\t', stringsAsFactors=F)

# Convert the percentage string columns into numeric values.
data[,3] <- as.numeric(sub("%", "", data[,3]))
data[,4] <- as.numeric(sub('$', '', as.character(data[,4]), fixed=TRUE))
data[,5] <- as.numeric(sub('$', '', as.character(data[,5]), fixed=TRUE))
data[,6] <- as.numeric(sub("%", "", data[,6]))
data[,7] <- as.numeric(sub("%B", "", data[,7]))
data[,8] <- as.numeric(sub("%", "", data[,8]))
data[,9] <- as.numeric(sub("%", "", data[,9]))
data[,10] <- as.numeric(sub("%", "", data[,10]))
data[,11] <- as.numeric(sub("%", "", data[,11]))

# Replace NA with 0.
data[is.na(data)] <- 0

With the data ready for processing, we can now split it into a training and test set. We’ll run K-means on our training set, to allow it to determine cluster categories for the data. Later on, we’ll run the trained model against our test set and see if it accurately classifies the new ETF funds under categories that make sense. The code for splitting the data set and running the clustering algorithm is shown below.

# Initialize a random seed for reproducibility.
set.seed(123)

# Split a train and test set.
data2 <- sample.split(data$Ticker, SplitRatio = .75)
train <- subset(data, sample == TRUE)
test <- subset(data, sample == FALSE)

# Run kmeans clustering on the data.
fit <- kmeans(train[,8:11], 5, nstart = 20)
train$group <- fit$cluster

# Display the funds, sorted by their assigned group.
train[order(train$group),]

Manually Labeling Clusters

Recall, with the colors example, we manually labeled the clusters to give them human-readable names and to better understand each category that was detected from the unsupervised learning clustering algorithm. We’ll do the same in this example, taking a peek at the data that was assigned to each group and give that group a specific category name.

Let’s take a look at the categorized results after clustering, to get an idea of what categories have been detected. Below is an excerpt of the training data, sorted by their assigned cluster.

"","Ticker","AssetClass","ExpenseRatio","Price","Change1","Change2","SECYield","YTD","Year1","Year5","Year10","Inception","group","label"
"10","VSS","International",0.13,107.67,0.17,0.15,0,15.5,19.61,9,0,"12.24% (04/02/2009)",1,"International"
"11","VEA","International",0.07,41.28,0.1,0.24,0,14.74,20.23,9.12,0,"1.17% (07/20/2007)",1,"International"
"12","VWO","International",0.14,41.19,0.29,0.71,0,16.02,18.85,3.32,1.58,"6.52% (03/04/2005)",1,"International"
"13","VGK","International",0.1,55.24,0.04,0.07,0,17.52,21.75,9.28,1.04,"4.63% (03/04/2005)",1,"International"
"2","VDC","Stock - Sector",0.1,138.44,-0.39,-0.28,2.46,4.68,2.6,12.8,10.33,"10.27% (01/26/2004)",3,"Stock"
"38","VNQ","Stock - Sector",0.12,81.18,-0.05,-0.06,0,0.04,-1.89,9.3,6.2,"9.06% (09/23/2004)",3,"Stock"
"48","VOX","Stock - Sector",0.1,89.37,-0.99,-1.09,3.5,-9.19,-3.43,10.16,4.42,"8.09% (09/23/2004)",3,"Stock"
"54","VPU","Stock - Sector",0.1,112.97,-0.07,-0.06,3.32,7.27,3.14,11.63,7.08,"10.09% (01/26/2004)",3,"Stock"
"5","VDE","Stock - Sector",0.1,88.06,0.49,0.56,2.69,-14.68,-4.55,0.64,0.65,"6.52% (09/23/2004)",4,"Bond"
"6","EDV","Bond - Long-term Government",0.07,114.97,0.45,0.39,0,6.48,-10.37,3.38,0,"8.24% (12/06/2007)",4,"Bond"
"22","VCIT","Bond - Inter-term Investment",0.07,87.31,0.12,0.14,0,3.47,1.1,4.04,0,"5.88% (11/19/2009)",4,"Bond"
"23","VGIT","Bond - Inter-term Government",0.07,64.51,0.1,0.16,0,1.64,-2.13,1.32,0,"3.02% (11/19/2009)",4,"Bond"
"29","VGLT","Bond - Long-term Government",0.07,75.94,0.16,0.21,0,4.44,-7.11,2.74,0,"6.55% (11/19/2009)",4,"Bond"
"1","VCR","Stock - Sector",0.1,140.79,-0.14,-0.1,1.29,10.14,18.24,17.06,9.9,"9.35% (01/26/2004)",5,"SmallMidLargeCap"
"7","VXF","Stock - Mid-Cap Blend",0.08,102.15,0.29,0.28,1.33,7.12,21.55,14.36,7.73,"9.49% (12/27/2001)",5,"SmallMidLargeCap"
"17","VHT","Stock - Sector",0.1,147.01,0.02,0.01,1.37,16.83,14.7,18.12,11.13,"9.78% (01/26/2004)",5,"SmallMidLargeCap"
"18","VYM","Stock - Large-Cap Value",0.08,77.95,-0.11,-0.14,3.09,4.49,12.73,13.64,7.08,"7.53% (11/10/2006)",5,"SmallMidLargeCap"

In the above output, we can see the data that was assigned to specific clusters. In fact, it looks like the categories make sense! Looking at the first cluster, we can see all of the rows that were assigned to it contain somewhat similar percentage returns, all within a generally similar range. Since we know that these particular ETFs are international funds, we can label this cluster with the name “International”.

Likewise, we can see similar groupings for percentages for Stocks, Bonds, and SmallMidLargeCap funds. Each of these categories of ETFs tends to have similar percentage returns, even though they originate from different funds. Our AI clustering algorithm has detected these similarities, grouping the rows of data accordingly.

The code for manually labeling the clusters and assigning the category name to the training data is shown below.

# Manually label the clusters with names (guessed by looking at the resulting clusters).
centroids <- as.data.frame(fit$centers)
centroids$group <- 1:nrow(centroids)
centroids$label <- c('International', 'StockBigGain', 'Stock', 'Bond', 'SmallMidLargeCap')

# Set assigned label on training data.
train$label <- centroids$label[train$group]

# Save the result to a csv file.
write.csv(train[order(train$group),], file='clustered.csv')

Predicting the Category for New ETFs

Now the exciting part happens! We’ve trained our unsupervised learning model on a training set of ETF funds, effectively assigning category names to each row of data. We’ve determined that the clusters are using similar ranges in percentage returns to group ETF funds together. The categories appear to, indeed, make sense.

The code for predicting categories for the test set is shown below.

# Predict on new data.
fit2 <- as.kcca(fit, data=train[,8:11])

# Predict the assigned color by mapping the color to a cluster.
test$group <- predict(fit2, newdata=test[,8:11])

# Assign the label of the cluster.
test$label <- sapply(1:nrow(test), function(row) {
  centroids[centroids$group == test[row, 'group'], ]$label
})

# Save the result to a csv file.
write.csv(test[order(test$group),], file='clustered2.csv')

Just as we did with the colors example, we’re calling the predict method, along with our trained model, to classify the test set data under our detected categories. We then apply the label to each row in the test set and write out a CSV file with the results for us to examine.

ETF Category Results

The results of applying the trained model to our test set is shown below. Each ETF has been classified under a specific category (cluster), listed in the last column, marked “label”. It’s interesting to see that the categories appear quite accurate!

Of course, ultimately, unsupervised learning and automatic assignment of categories can be subjective in nature. The categories selected for each piece of data by the artificial intelligence algorithm might not match exactly to what a human would select. This is the nature of unsupervised learning, in general, yet it still can serve as a valuable and powerful tool for understand data with machine learning technologies.

"","Ticker","AssetClass","ExpenseRatio","Price","Change1","Change2","SECYield","YTD","Year1","Year5","Year10","Inception","group","label"
"9","VEU","International",0.11,50.15,0.18,0.36,0,15.09,20.1,7.54,1.47,"2.72% (03/02/2007)",1,"International"
"15","VNQI","International",0.15,55.7,-0.05,-0.08,0,12.94,8.84,7.77,0,"5.68% (11/01/2010)",1,"International"
"51","VXUS","International",0.11,52.06,0.18,0.35,0,15.11,20.19,7.68,0,"3.68% (01/26/2011)",1,"International"
"27","BLV","Bond - Long-term Investment",0.07,92.18,0.08,0.09,0,5.38,-1.18,4.15,7.59,"7.23% (04/03/2007)",3,"Stock"
"4","VWOB","International",0.32,79.42,0.03,0.03,0,4.76,4.51,0,0,"4.70% (05/31/2013)",4,"Bond"
"21","BIV","Bond - Inter-term Investment",0.07,84.2,0.13,0.15,0,2.61,-1.15,2.62,5.6,"5.38% (04/03/2007)",4,"Bond"
"28","VCLT","Bond - Long-term Investment",0.07,92.55,0.04,0.04,0,5.8,2.89,5.37,0,"7.89% (11/19/2009)",4,"Bond"
"40","BSV","Bond - Short-term Investment",0.07,79.78,0.05,0.06,0,1.16,-0.01,1.17,2.88,"2.87% (04/03/2007)",4,"Bond"
"3","VIG","Stock - Large-Cap Blend",0.08,92.39,-0.21,-0.23,1.93,9.62,13.75,12.75,7.41,"7.92% (04/21/2006)",5,"SmallMidLargeCap"
"16","VUG","Stock - Large-Cap Growth",0.06,127.51,0.09,0.07,1.32,15.13,20.19,14.87,8.81,"8.41% (01/26/2004)",5,"SmallMidLargeCap"
"33","MGV","Stock - Large-Cap Value",0.07,69.26,-0.16,-0.23,2.54,4.49,15.71,14.1,0,"6.45% (12/17/2007)",5,"SmallMidLargeCap"
"39","VOO","Stock - Large-Cap Blend",0.04,222.42,-0.18,-0.08,1.97,9.41,17.86,14.59,0,"14.79% (09/07/2010)",5,"SmallMidLargeCap"
"45","VBK","Stock - Small-Cap Growth",0.07,145.75,0.69,0.48,0.91,9.95,18.99,12.91,7.89,"8.92% (01/26/2004)",5,"SmallMidLargeCap"
"52","VTI","Stock - Large-Cap Blend",0.04,124.56,-0.05,-0.04,1.86,9.04,18.49,14.55,7.39,"6.69% (05/24/2001)",5,"SmallMidLargeCap"

Download @ GitHub

The source code for this project is available on GitHub.

About the Author

This article was written by Kory Becker, software developer and architect, skilled in a range of technologies, including web application development, machine learning, artificial intelligence, and data science.

Sponsor Me