Intelligent Heuristics for the Game Isolation using AI and Minimax

Introduction

How do you create an intelligent player for a game? Artificial intelligence offers a variety of ways to program intelligence into computer opponents. In this article, we’ll show how it works, using intelligent heuristics and a web-based game that you can try yourself.

Artificial intelligence is becoming an increasingly important topic in the field of computer science. While advancements in machine learning continue to break records in areas including image recognition, voice recognition, translation, and natural language processing, many additional branches of AI continue to advance as well. One of the earliest applications of AI is in the area of game development. Specifically, artificial intelligence is often used to create opponent players in games.

Early forms of AI players in games often consisted of traditional board games, such as chess, checkers, backgammon, and tic-tac-toe. Games of this type provide a fully observable and deterministic view at any point in the state of the game. This allows an AI player the ability to analyze all possible moves from both the human player and the AI player itself, thus determining the best likely move to take at any given time.

AI players in video games have since expanded to a much broader range of gaming categories, where the best move or course of action is not always crystal clear. These include games that often utilize random events or actions, in addition to hidden views of the game or of the opponent’s actions. Games of this type often include role-playing games, multiplayer games, card games, and many more.

In this tutorial, we’ll walk through how to create an artificial intelligence agent for the game, Isolation. We’ll demonstrate how to create a basic version of the game that can be run in a web page, using HTML, CSS, and React JavaScript. We’ll also demonstrate how to create an artificial intelligence AI driven player by using the Minimax algorithm with Alpha-beta pruning.

Before we get started with the code, let’s take a look at the rules of the game, Isolation.

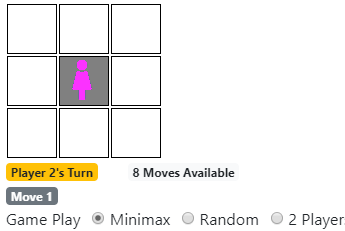
Play the Game Online

You can play the game Isolation online in your web browser.

Try changing the setting for the AI’s game play to Minimax, Random, or 2 Players to see the differences in how the game operates.

In particular, you can notice the distinct change in difficulty from when the AI computer opponent plays randomly, compared to when using the artificial intelligence algorithm of Minimax with alpha-beta pruning.

You can also change the heuristic strategy that the AI player uses, which changes the level of difficulty. Various heuristic strategies are discussed later in the tutorial.

What is Isolation

Isolation is a board game that looks similar to a checker board. The game is played on a grid, for example 3x3 in size. The first player chooses a cell to start. Each player takes turns moving their player to a new cell. A player can move to any cell with a clear path, up, down, left, right, or diagonal, as long as the path is not blocked by a previously visited cell or by the other player. If a player is unable to make any further move, the opponent wins. Thus, the goal of the game is to be the last player with a remaining move available.

A screenshot of the game is shown below.

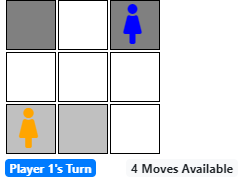
Notice, in the above screenshot, both players have made moves. It’s currently player one’s turn, with four valid moves available. Player one can move left one cell, down one or two cells, or down-left one cell. The player can not make any other moves due to previously cells blocking the path.

A winning screenshot of the game is shown below.

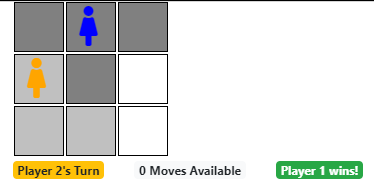
Notice, in the above screenshot, Player 1 has a single valid move available, by moving down-right. However, Player 2 is completely isolated and has no valid moves available. In this case, Player 1 wins.

Fully Observable, Deterministic, and Adversarial

The game Isolation was selected for this tutorial as it is a fully observable and deterministic game. That is, the entire game board can be seen at any given time, including the positions of both players and all previously visited cells. Additionally, since randomness of actions is not used within the game, the game’s states are deterministic, as opposed to stochastic, where a move may have a random effect. In this manner, all available moves at any given point in the game can be analyzed.

In addition to Isolation being fully obserable and deterministic, the game is also adversarial. Games that involve two players competing against one another to win, are considered adversarial in nature. Each player is attempting to prevent the other player from winning, in addition to maximizing their chance of winning the game.

It’s these specific conditions that allow the design of an intelligent agent through the use of the AI minimax algorithm.

Minimax Algorithm

Minimax is an artificial intelligence AI algorithm that allows us to find the best move for a player. It works by seeking to maximize the score for the player, while at the same time, minimizing the score for the opponent. In order to do this, the minimax algorithm requires a game to be fully observable, deterministic, and adversarial. At each move in the game, the minimax algorithm walks through a game tree of available player actions and their resulting states, calculates the score for each new state, and applies an operation of maximizing the score or minimizing the score at each level of the game tree, according to which player’s turn it is.

Consider the following example. Suppose that we have a game tree, consisting of all possible actions and their resulting states for the current condition of the game board. Each state is assigned a score, depending on how favorable the position is to the player. Our game tree appears, as shown below.

      [ ]
      / \
   [ ]   [ ]
/ \ / \ / \ / \
[4] [2] [6] [8]

Since we can’t know a score for the player until we reach an ending state of the game tree, only the leaf nodes have score values. In the above game tree, we can see that there are 4 terminal states, each with their own corresponding score for the player.

At first glance, it’s obvious that the player should select the bottom-right node. The player would do this by taking all moves, starting from the top root node, down and towards the right, until they get to the score of 8. However, remember that the opponent gets to take a turn at each step. Therefore, after the player selects their first action, their opponent will likely take a different action than the original player planned, in order to prevent the player from getting to the game state with a score of 8. Therefore, when planning which action is the best one for the player to make, we need to consider the opponent’s moves and plan accordingly.

To choose the best action (node), we start from the bottom and work our way up in a recursive fashion.

We’ll make the top root node as a “max” node, since it’s the referernce player’s turn that we’re trying to find the best move for. After the reference player makes a move, it will be the other player’s turn. We’ll set the next level of nodes to “min” nodes. We repeat this process of assigning “min” and “max” layers to the nodes until we reach the bottom of the game tree. Now we can select nodes accordingly.

At level two in the game tree, we are at a “min” level. This means that it’s actually the opponents turn to choose an action. According to the game tree, the left-most branch offers two potential actions for the other player (4, 2). Since it’s the opponents turn (“min” layer), we assume they will choose the best move for themselves, which is to minimize the reference player’s score. Therefore, they will chose the node with value 2.

We repeat the above process for the second branch, containing 6 and 8. The opponent will minimize this score by choosing the state with a score of 6 for the other player.

At this point, our game tree appears as shown below.

      [ ]    Max
      / \
   [2]   [6]      Min
/ \ / \ / \ / \
[4] [2] [6] [8]

At the top layer, it is the reference player’s turn. Thus, we are at a “max” layer. We’ll choose from the available game actions that will result with the best score from what our opponent has left us with. In this case, we’ll select the action that gives us a score of 6.

      [6]    Max
      / \
  [2]     [6]      Min
/ \ / \ / \ / \
[4] [2] [6] [8]

We’ve now completed running the minimax artificial intelligence AI algorithm and have selected the best move for the player as being the one that achieves a score of 6.

If the reference player follows the series of actions to achieve the target node with a score of 6 (and the opponent plays a perfect game, always choosing their own best moves, as we expect from the game tree), then we can plan on the reference player being able to achieve the target outcome.

There are a variety of great descriptions of the minimax algorithm available for further detail.

Let’s take a look at one additional optimization that can be made to minimax to allow it to run even faster.

Minimax with Alpha-beta Pruning

Minimax requires building a game tree in order to evaluate all possible states and their resulting scores for the player. Building this tree is one of the most expensive parts for implementing the minimax algorithm within a game. Naturally, we want to minimize any wait or lag between turns in order to make the game-play as smooth as possible. Therefore, it’s important to optimize both the game tree building and execution of the minimax algorithm as much as possible to improve the speed of AI.

One method for increasing the performance of the minimax algorithm is to avoid the need to analyze all nodes of the game tree. This can be done by effectively pruning away nodes which would not be selected by the particular player who’s turn it is.

Alpha-beta pruning gives the same result as the minimax algorithm described above, but does so by evaluating less states.

A description of the alpha-beta pruning algorithm is available.

For this tutorial, let’s take a look at the implementation of minimax with alpha-beta pruning and of the game Isolation, developed in JavaScript.

Creating a Web-Based Version of the Game Isolation

To begin, we’ll use React and JavaScript to create a web-based version of the game Isolation. It will be playable in the web browser, with the grid, cells, and players drawn using CSS and HTML tables. We begin by creating an empty container to host the React application.

<div class='container'>
  <div id='root'></div>
</div>

In the above code, we’ve simply created an empty div with the name “root” to hold our React application and render the HTML components.

Next, we’ll create our initial instantiation of the React application and of our Isolation board game into the container. We can do this with the following React code to render our game component.

// Main React render hook.
$(function() {
  const isolationCtrl = ReactDOM.render(
    <div>
      <IsolationContainer width="3" height="3"></IsolationContainer>
    </div>,
    document.getElementById('root')
  );
});

The above code initializes the game Isolation with a grid size of 3x3. It actually renders an IsolationContainer component, which contains controls and settings for adjusting the width, height, and various settings for the AI player.

Creating a Cell

With the Isolation game container created, let’s take a look at how the cells and grid are rendered in React. We’ll start with an individual cell.

class Cell extends React.Component {
  constructor(props) {
    super(props);

    this.onClick = this.onClick.bind(this);
  }

  onClick(e) {
    // Callback handler for cell click event.
    this.props.onClick(this, this.props.x, this.props.y);
  }

  render() {
    return (
      <div id={ `cell-${this.props.x}-${this.props.y}` } className={`cell ${this.props.cellStyle || ''}`} style={{width: this.props.width || '', height: this.props.height || '', backgroundColor: this.props.color }} onClick={ this.onClick }>
        { this.props.children }
      </div>
    );
  };
}

The above code renders a div element for each cell within the grid. In the case of a 3x3 grid, we’ll render nine instances of the cell component in React. Each cell contains a click event handler, along with the ability to render child components contained within the cell (such as the player icon component). When a cell is clicked, it sends an event to the parent component, passing in the coordinates of the clicked cell. In this way, the parent component (the grid) knows which cell was clicked and can update its internal memory accordingly, thus moving the position of the players and marking visited cells.

Creating a Grid

The grid component consists of an array of cells. The component maintains an internal state of the cells, thus recording which cells have been visited, along with the positions of the players.

An excerpt from the Grid javascript React code is shown below. Notice how the constructor initializes the array of cell values with 0, indicating empty cells at the start of the game.

class Grid extends React.Component {
  constructor(props) {
    super(props);

    const values = props.grid || [];
    if (!props.grid) {
      // Populate the grid values with zeros.
      for (let y=0; y <= props.height; y++) {
        const row = [];
        for (let x=0; x <= props.width; x++) {
          row.push(0);
        }

        values.push(row);
      }
    }

    this.state = {
     values,
     width: props.width,
     height: props.height,
    };
  
    // ...
  }
}

When a cell is clicked, the Cell React component passes the coordinates of the cell to the Grid component. The Grid component, in turn, passes this click event up to the Isolation component, which manages the core rules for the game. The code below shows where the click event is propagated back up to the parent Isolation component, which is hosting the Grid object.

onClick(cell, x, y) {
    // Callback handler for cell click event.
    this.props.onClick(x, y, this.state.values, cell);
}

In the above code, the Grid component passes the click event to the parent component, which will end up calling the setValue() method to update the internal state of the grid.

The code for updating the internal state for the grid, by marking the cell as visited by a player, is shown below.

setValue(x, y, value) {
  // Set the cell value.
  const values = this.state.values;
  values[y][x] = value;

  this.setState({ values });
}

Finally, we render the array of cells and draw the full grid by looping through the width and height of the grid and rendering a cell component for each one.

render() {
  const rows = [];
  for (let y=0; y<this.state.height; y++) {
    const cols = []
    for (let x=0; x<this.state.width; x++) {
      cols.push(
        <td>
          <Cell x={x} y={y} color={ this.state.values[y][x] } cellStyle={ this.props.cellStyle } onClick={ this.onClick }>
            { this.props.players.map((player, index) => {
              return (x === player.x && y === player.y) ? this.props.children[index] : null
            }) }
          </Cell>
        </td>
      );
    }

    rows.push(<tr>{cols}</tr>);
  }

  return (
    <div class='grid'>
      <table>
        <tbody>
          {rows}
        </tbody>
      </table>
    </div>
  )
}

Notice in the above code, we’re also conditionally rendering a child component based upon the location of the players. When a player should be located within a cell, we render the child component (a Player component). This allows drawing the player icons within the correct cells on the grid.

Drawing the Player

The player is a simple React component, consisting of an HTML icon. We draw the player within a cell using the code shown below.

class Player extends React.Component {
  constructor(props) {
    super(props);
  }

  render() {
    // Adjust offset to position player icons on grid.
    let leftOffset = 25;
    let topOffset = 5;
    const container = $('#app');
    if (container.length) {
      const rect = container[0].getBoundingClientRect();
      leftOffset = rect.left + 15;
      topOffset = rect.top + 5;
    }

    return (
      <i class={ `player ${this.props.cellStyle || ''} fas fa-female` } style={{ top: `${this.props.y * this.props.height + topOffset}px`, left: `${this.props.x * this.props.width + leftOffset}px`, color: this.props.color }}></i>
    );
  }
}

Notice, in the above code we’re simply rendering an icon HTML element to represent each player in the game.

Putting It All Together

The key part of implementing Isolation in React in the web browser is the Isolation component. This component renders the grid, along with two player components as children of the grid. The component also handles the click event from the grid (and the corresponding cell), determines if the move is valid according to rules of the game, and calls setValue() on the grid accordingly.

An excerpt from the code is shown below, which handles the click event and determining if the given move is valid.

class Isolation extends React.Component {
  // ...

  onGrid(x, y, values) {
    const playerIndex = this.state.playerIndex;
    const players = this.state.players;

    if (IsolationManager.isValidMove(x, y, playerIndex, players, values, this.grid.current.props.width, this.grid.current.props.height)) {
      // Update player position.
      players[playerIndex].x = x;
      players[playerIndex].y = y;

      // Update the grid local variable with the player move (so available moves will be accurate).
      values[y][x] = playerIndex + 1;

      // Update available moves for all players.
      players[0].moves = IsolationManager.availableMoves(0, players, values, this.grid.current.props.width, this.grid.current.props.height);
      players[1].moves = IsolationManager.availableMoves(1, players, values, this.grid.current.props.width, this.grid.current.props.height);

      // Update cell value in the grid.
      this.grid.current.setValue(x, y, !playerIndex ? 'gray' : 'silver');
      // ...
    }
  }
}

In the above code, we’ve received a click event from the grid (and thus from a given cell). We first determine if the move is valid by passing the coordinate on the grid to our IsolationManager game logic. This manager class contains all associated logic for handling rules of the game. It also serves as a convenient manager class for changing the rules of the game or to implement different versions of the game.

After we’ve determined a valid move, we update the moves for each player by calculating all possible moves from the current state. This is necessary in order to build the resulting game tree and calculate the minimax result for the current board state for the artificial intelligence AI player.

After updating the moves, we set the new state for the component and allow the AI player to take their turn. The code shown below, demonstrates how the artificial intelligence AI player takes their turn. The code first determines whether the game mode is set to two players and if an AI strategy has been defined. It then executes the AI manager strategy (for example, random or minimax algorithms) in a separate thread, which allows for the web page to remain responsive while the AI calculates its move.

// Update state and play opponent's turn.
this.setState({ round: this.state.round + 1, playerIndex: !playerIndex ? 1 : 0, players }, () => {
  if (this.state.playerIndex && this.state.players[this.state.playerIndex].moves.length > 0) {
    if (this.state.strategy && this.state.strategy !== StrategyManager.none) {
      // AI turn.
      setTimeout(() => {
        const tree = StrategyManager.tree(playerIndex, JSON.parse(JSON.stringify(players)), values, this.grid.current.props.width, this.grid.current.props.height);
        StrategyManager.renderTree(tree, this.state.treeDepth);

        // Get the AI's move.
        ({ x, y } = this.props.strategy(tree, this.state.playerIndex, this.state.players, values, this.grid.current.props.width, this.grid.current.props.height));
        console.log(`AI is moving to ${x},${y}.`)

        // Move the AI player.
        this.onGrid(x, y, values);
      }, 1000);
    }
  }
});

Notice in the above code, we build a game tree using the helper method StrategyManager.tree(). This is the most expensive operation in the AI algorithm, as part of minimax. The tree is required in order to analyze all available game states, starting from the current state of the game board, through to the end. Since the game is fully observable and deterministic, the AI can calculate the best course of action, using the minimax algorithm, and select which move to make next.

As an added bonus, we can render a graphical representation of the game tree by using the StrategyManager.renderTree() method. This method takes advantage of React by re-using the Grid component to render a smaller version of the grid for each potential game state within the tree. This is one of the beauties of using React - reusing components in other areas of the application!

AI Strategy

Within the IsolationManager class, we implement the AI logic using a strategy design pattern. In this manner, we can implement different strategies for the AI player to implement, while keeping them separate and easily maintainable in the code.

The Random Strategy

Our AI can utilize a random strategy, which simply chooses a random valid cell to move to, without considering any logic for score or out-smarting the human player.

The code for implementing the random strategy is shown below.

random: function(tree, playerIndex, players, values, width, height) {
  let isValid = false;
  let count = 0;
  let x, y;

  while (!isValid && count++ < 1000) {
    x = Math.floor(Math.random() * width);
    y = Math.floor(Math.random() * height);
    isValid = IsolationManager.isValidMove(x, y, playerIndex, players, values, width, height);
  }

  if (count >= 1000) {
    // Random strategy failed to find a move.
  }

  return { x, y };
}

Notice, the above code simply chooses a random x,y location and continues choosing randomly until a valid move is discovered.

However, the real intelligence comes from the strategy implemented for minimax, which applies the minimax algorithm with alpha-beta pruning to the game tree in order to intelligently determine the best move for the AI player.

The Minimax and Alpha-Beta Pruning Strategy

The minimax algorithm with alpha-beta pruning is implemented in JavaScript and allows the AI to intelligently choose the best move for the AI player at each turn. The JavaScript code below was adapted from an original implementation in Python. The code is shown below.

minimax: function(tree, playerIndex, players, values, width, height) {
  let bestState = null;
  let bestVal = -9999;
  let beta = 9999;

  const getSuccessors = node => {
    return node ? node.children : [];
  };

  const isTerminal = node => {
    return node ? node.children.length === 0 : true;
  };

  const getUtility = node => {
    return node ? node.score : -9999;
  };

  const maxValue = (node, alpha, beta) => {
    if (isTerminal(node)) {
      return getUtility(node);
    }
    else {
      let value = -9999;

      const successors = getSuccessors(node);
      successors.forEach(state => {
        value = Math.max(value, minValue(state, alpha, beta));
        if (value >= beta) {
          return value;
        }
        else {
          alpha = Math.max(alpha, value);
        }
      });

      return value;
    }
  };

  const minValue = (node, alpha, beta) => {
    if (isTerminal(node)) {
      return getUtility(node);
    }
    else {
      let value = 9999;

      const successors = getSuccessors(node);
      successors.forEach(state => {
        value = Math.min(value, maxValue(state, alpha, beta));
        if (value <= alpha) {
          return value;
        }
        else {
          beta = Math.min(beta, value);
        }
      });

      return value;
    }
  };

  const successors = getSuccessors(tree);
  successors.forEach(state => {
    const value = minValue(state, bestVal, beta);
    if (value > bestVal) {
      bestVal = value;
      bestState = state;
    }
  });

  return bestState ? { x: bestState.players[bestState.activePlayer].x, y: bestState.players[bestState.activePlayer].y } : { x: 1, y: 1 };
}

The above code first implements the helper methods required for using the minimax algorithm. These include the getSuccessors function, which simply returns the current node’s child nodes. We’ve also implemented an isTerminal function, which determines if a node is a leaf node (meaning we can begin calculating the minimax score by walking up the game tre from this node). We’ve also implemented a getUtility function, which returns the score for the current node.

As we’ve described above, the minimax algorithm is implemented by choosing the max of the min values at each level set in the game tree, applying each players alternate moves against the game board to find the best move for the active player. In this way, we’ve implemented a maxValue and minValue function which performs this logic on the current node and its children.

Building the Game Tree

In order to utilize the minimax artificial intelligence AI algorithm with alpha-beta pruning, we need to create a game tree after each player move in the game.

A game tree is constructed by starting at the current game board state. We then get a list of all available moves for the current player and apply them to the current board state. We take the resulting list of child states and continue this process for each one, effectively building a tree of game board states. This continues until we reach the terminal leaf nodes for the game state (i.e., the end of the game for one of the players) or we exceed the maximum depth for our calculation.

It’s important to note that the tree function takes a parameter maxDepth. This value indicates how far into the game tree that we’re willing to analyze and build. Since this method is the most time-consuming and demanding process of minimax, it’s important to optimize the depth into the game tree that we build, in order to minimize the lag time while waiting for the AI player to choose the next move to make.

Another important aspect of the game tree is assigning a score value to each game board state (node). This allows us to indicate to the AI how good or bad a particular state is. This key piece of information will be used by the minimax algorithm when determining which nodes to take for the AI player.

The score value for each game board state is determined using an intelligent heuristic, a key part of any artificial intelligence strategy within a game, and is indicated by the parameter heuristic which is passed into the tree function. This parameter is actually a function call, which will execute one of the methods from the HeuristicManager class in order to obtain a score for the given node. Details of the various heuristic methods are described later in this tutorial, as this score is one of the key concepts for the AI in the game and for the minimax algorithm. After all, the heuristic score for each node in the game tree dictates which action the AI will favor when selecting a move to make, and thus, the end behavior of the AI’s game-play.

The code for building the game tree is shown below.

tree: function(playerIndex, players, values, width, height, round, heuristic, maxDepth = 4) {
  const referencePlayerIndex = !playerIndex ? 1 : 0; // Point-of-view for the player that the tree is calculated for. The root node will be from the opposing player.
  
  let root = { depth: 0, player: playerIndex, activePlayer: playerIndex, baseScore: players[referencePlayerIndex].moves.length, score: heuristic(players[referencePlayerIndex].moves.length, players[!referencePlayerIndex ? 1 : 0].moves.length, width, height, round), moves: players[referencePlayerIndex].moves, players, values, children: [], width, height };
  let fringe = [ root ];
  let node = fringe.shift();

  while (node) {
    if (node.depth <= maxDepth && node.moves.length) {
      const newPlayerIndex = node.depth % 2 === 0 ? referencePlayerIndex : playerIndex;

      // Evaluate all possible moves from the current state.
      node.moves.forEach(move => {
        // Make a copy of the players.
        let newPlayers = JSON.parse(JSON.stringify(node.players));

        // Move the player to a new position.
        newPlayers[newPlayerIndex].x = move.x;
        newPlayers[newPlayerIndex].y = move.y;

        // Set the new position as used.
        let newValues = JSON.parse(JSON.stringify(node.values));
        newValues[newPlayers[newPlayerIndex].y][newPlayers[newPlayerIndex].x] = !newPlayerIndex ? 'gray' : 'silver';

        // Get available moves at new position in relation to the reference player.
        const movesReferencePlayer = IsolationManager.availableMoves(referencePlayerIndex, newPlayers, newValues, width, height);
        // Get available moves with new game board for next player.
        const moves = IsolationManager.availableMoves(!newPlayerIndex ? 1 : 0, newPlayers, newValues, width, height);

        // Add the new node to our tree.
        const child = { depth: node.depth + 1, player: playerIndex, activePlayer: newPlayerIndex, baseScore: movesReferencePlayer.length, score: heuristic(movesReferencePlayer.length, moves.length, width, height, round), moves, players: newPlayers, values: newValues, children: [] };
        node.children.push(child);
        fringe.push(child);
      });
    }

    // Process next node.
    node = fringe.shift();
  }

  return root;
}

The above code begins with a root node and then determines all available moves from the current state. Each possible valid move is added as a child node to the root. We repeat this process in a breadth-first search manner, moving deeper into the game tree, as we discover more valid actions and child nodes. We provide a cut-off depth in order to control how far down into the game tree we go, before stopping in order to provide a timely response to the player.

An alternative implementation with this type of search that can optimize the breadth-first and depth-first search operation is called iterative deepening. Iterative deepening combines breadth-first and depth-first search and is used in instances when not enough memory is available for a complete breadth-first search and slower performance is acceptable.

One advantage to using React to implement the Isolation game board is that we’re able to re-use the Isolation component to render the game tree itself on the web page.

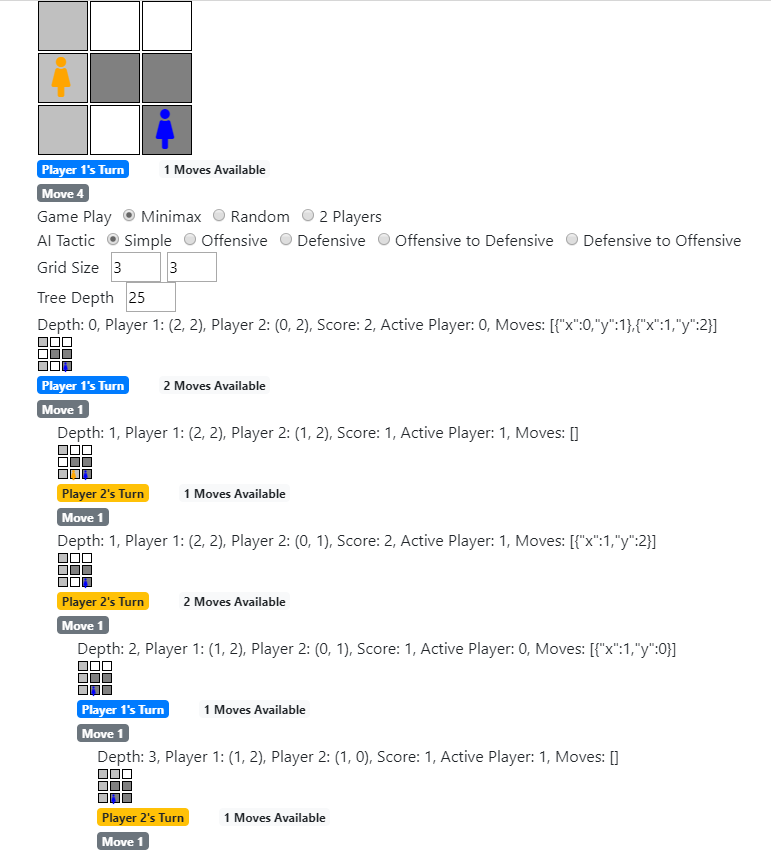
Game Rules and Logic

The core game rules and associated logic for Isolation are implemented within the IsolationManager javascript class. This largely consists of a check for valid moves, by enumerating across all potential cells, looking for blocked cells within the path. The resulting array of valid moves are returned, allowing the implementation of the game tree and updating of moves for each player.

Adding Intelligence to the AI

One of the key pieces for implementing the minimax algorithm for the artificial intelligence AI player is to apply a heuristic function.

Recall, we’re building a game tree for each possible action and resulting state of the game. Within each of these states (nodes) we assign a score value, corresponding to how beneficial the state is for the referenced player. This, in turn, will dictate which game action to take next. In order to do this, we need to apply some manner of intelligent heuristic that chooses how good or bad a particular node is.

What is a Heuristic?

A heuristic is information that allows a computer program to learn and behave with, seemingly, human intelligence. Heuristics are used within the minimax algorithm in order to determine the score for a given state in the game tree (node). Without this key piece of information, all states within the game tree would appear equal, and the AI computer player would have no way to decide which move would be best.

By applying a heuristic function to each state in the game tree, we can allow the minimax algorithm to walk through the nodes, starting from the terminal leaf nodes, working its way back up to the root, and thus back to the current state of the current game board. The minimax AI algorithm can then analyze the heuristic scores and return the resulting best move for the AI player to take.

In our implementation of Isolation, we’ll implement several different types of heuristic functions. This will allow our artificial intelligence AI player to use a variety of strategies against the human opponent. Our strategies will range from a simple count of available moves, to including information with regard to how many moves the opponent has as well. We’ve even included some heuristic functions that take the length of the game into consideration and alter the strategy of the AI player based upon early and late-game goals.

Let’s begin by looking at the simplest strategy.

The Simple Strategy

Since the heuristic is the key piece of intelligent information that we’re providing to our AI player, in order to analyze the game board states and determine which one is the next best move to take, it’s important to put considerable thought into the types of heuristics that we implement.

If a poor heuristic is given, our AI player will likewise perform poorly. Worse, the AI player may just appear to be playing randomly, which would not give much of a challenge to the opponent.

Let’s start with one of the simplest, and perhaps, most obvious strategies - counting the number of available moves for the player.

In the simple strategy heuristic for the game Isolation, we can simply count how many moves the player has available to them in the current state. If the player can move to five different cells in the current board state, we could assign a score of five to that state. Likewise, if the player has no available moves left, we would assign a score of zero. An artificial intelligence agent using this heuristic strategy as part of the minimax algorithm would thus prefer actions in the game that result in the AI having the most available moves. The AI would not care or consider how many moves the opponent player might have. This could be considered a “greedy” game-play strategy and can be implemented as shown below.

simple: function(playerMoves) {
  // Favor maximizing the number of available moves for the player.
  return playerMoves;
}

Notice, we’re simply returning the number of available moves for the player as our score for the current board state node in the game tree. We’re not considering, at all, how many moves the opponent may have available. Nor are we considering how far into the game we’ve played or any other aspect of the game.

As it turns out, this is actually quite an effective game play strategy. By maximizing the number of available moves, the AI player can ensure that they always try to have at least one remaining move available. The hope is that their opponent runs out of moves before they do.

The Defensive Strategy

Moving beyond a simple greedy strategy, another option is to have the AI player favor retaining the most number of available moves, while also taking into account minimizing the human player moves. We can apply a weighted score to the AI’s available moves in order to indicate its importance and then take the difference between this value and the opponent’s number of available moves. In this manner, the AI will favor making a move when it results in the opponent having the least number of moves available to them and the AI player having the most. This effectively implements a defensive strategy, since we’re attempting to maximize the number of moves available, while trying to limit the opponent as best that the AI can.

defensive: function(playerMoves, opponentMoves) {
  // Favor maximizing the number of available moves for the player weighted while minimizing the available moves for the opponent, emphasis on maximizing the player.
  return (playerMoves * 2) - opponentMoves;
}

Notice, in the above code we’re weighting the number of available moves for the AI, while subtracting the number of moves available to the opponent. This has the affect of seeking to maximize the AI’s available moves.

Consider the case where the AI has the choice between two valid moves A and B. Both A and B result in five available moves for the AI. However, move A would result in the human player having three moves left available, while move B would result in the human player having two moves available.

Move	AI	Human	Heuristic	Score
A	5	3	(5*2)-3	7
B	5	2	(5*2)-2	8

The above table shows the number of moves available to the AI and the opponent for two different moves, A and B. A score is calculated using the ‘defensive’ heuristic for each move.

We can apply the heuristic calculation for defensive to assign a score for the two choices.

Since (5 * 2) - 3 = 7 < (5 * 2) - 2 = 8, it’s clearly advantageous for the AI to take move B, since it maximizes the AI’s available moves while, at the same time, putting the human player in a worse position, with less moves available. This is done by taking the difference between the player’s moves available and the opponent’s. We apply a weight to the player’s moves in order to favor the AI’s available move count, thus implementing a defensive heuristic.

The Offensive Strategy

Likewise, we can apply an offensive strategy by favoring putting the opponent in the worst possible position, even at the cost of reducing the available moves for the AI player. This offensive strategy is shown below.

offensive: function(playerMoves, opponentMoves) {
  // Favor maximizing the number of available moves for the player while minimizing the available moves for the opponent, emphasis on minimizing the opponent.
  return playerMoves  - (opponentMoves * 2);
}

Notice, in the above code, we’ve shifted the weight over to the opponent move count. In this manner, we’re now favoring minimizing the number of moves that the human player can make. This results in the AI playing more aggressively, in that the AI will choose to jeapordize its position for available moves in order to reduce the number of moves available to the opponent.

A Defensive to Offensive Strategy

If we consider the number of total moves left in the game within our heuristic, we can apply a sense of time to the Isolation game and alter the AI’s strategy of game-play according to how many moves are left in the game. This can achieve a more intelligent or surprising AI implementation, since the strategy being played changes over the course of the game. It also allows the artificial intelligence agent to play more dynamic, and perhaps, seem more natural with the moves that it makes over the course of the game.

defensiveToOffensive: function(playerMoves, opponentMoves, width, height, round) {
  // Early game, play a defensive strategy. Late game, play an offensive strategy.
  const ratio = round / (width * height);
  return ratio <= 0.5 ? HeuristicManager.defensive(playerMoves, opponentMoves) : HeuristicManager.offensive(playerMoves, opponentMoves);
}

Notice, in the above code we are now taking into account a ratio value. This corresponds to how far into the game we’ve played. The calculation takes the current round and divides it by the number of cells in the game board (width * height). If our game board is of size 3x3, we will have a total of nine cells. If both players play perfectly, there can be a total of nine moves until the game ends. Therefore, if we take the current round number and divide it by the total cells, we can obtain a ratio from zero to one, indicating how far into the game we’ve currently played.

When ratio <= 0.5, we can consider this the beginning/early part of the game. Likewise, when ratio > 0.5, we can consider this near the end of the game. We adjust the type of strategy used by the AI according to these two ranges, offering the AI the ability to play defensively in the early game, while switching to offensively late game.

The defensive to offensive strategy tends to be particularly effective in the game Isolation.

An Offensive to Defensive Strategy

Similar to our strategy for switching between defensive and offensive strategies, based upon the current round in the game, we can reverse the strategy to allow the AI to play offensive to defensive instead. In this manner, the AI player will start right away with an offensive strategy, attempting to attack the human player and reduce their available moves as much as possible, immediately upon the onset of the game. As the game continues and less cells are available to the players, the AI player will switch over to a defensive strategy in an attempt to our-last the human player for available moves.

offensiveToDefensive: function(playerMoves, opponentMoves, width, height, round) {
  // Early game, play an offensive strategy. Late game, play a defensive strategy.
  const ratio = round / (width * height);
  return ratio <= 0.5 ? HeuristicManager.offensive(playerMoves, opponentMoves) : HeuristicManager.defensive(playerMoves, opponentMoves);
}

Notice, in the above code we’re taking into account a ratio value, just as we did in the defensive to offensive heuristic. The only change to this particular heuristic is in the order of calling offensive() versus defensive() according to the ratio range.

Discovering Heuristics

While the game Isolation can appear quite simple in nature, in that the rules of the game are minimal, it still allows a range of different strategies and heuristics that can be analyzed to see how well they perform against both human and other AI players.

Various strategies and their corresponding win factors are described in Search Heuristics for Isolation, which details implementations of varying Isolation heuristics and their effects. Included in the paper are the dynamic strategies for switching between defensive and offensive and their comparisons to other heuristic functions and methods of game-play.

Can you think of any other effective game strategies for Isolation?

Download @ GitHub

The source code for this project is available on GitHub.

The game can also be played online or edited on CodePen.

About the Author

This article was written by Kory Becker, software developer and architect, skilled in a range of technologies, including web application development, artificial intelligence, machine learning, and data science.

Sponsor Me